Probabilistic Roadmaps
The following project is a simple implementation of a path planner for a robot. It combines global navigation and local navigation.
Note: Execute the Test Main script and change the file name and folder to run the program.
Global Navigation
The global navigation is solved using PRM (Probabilistic Roadmap Method) that generates samples in a map, joins them creatign a graph and then we navigate to our objective through the shortest path (if it exists).
In my implementation I have considered the map to be a grid map so that a pixel in the map is either free or occupied by an obstacle.
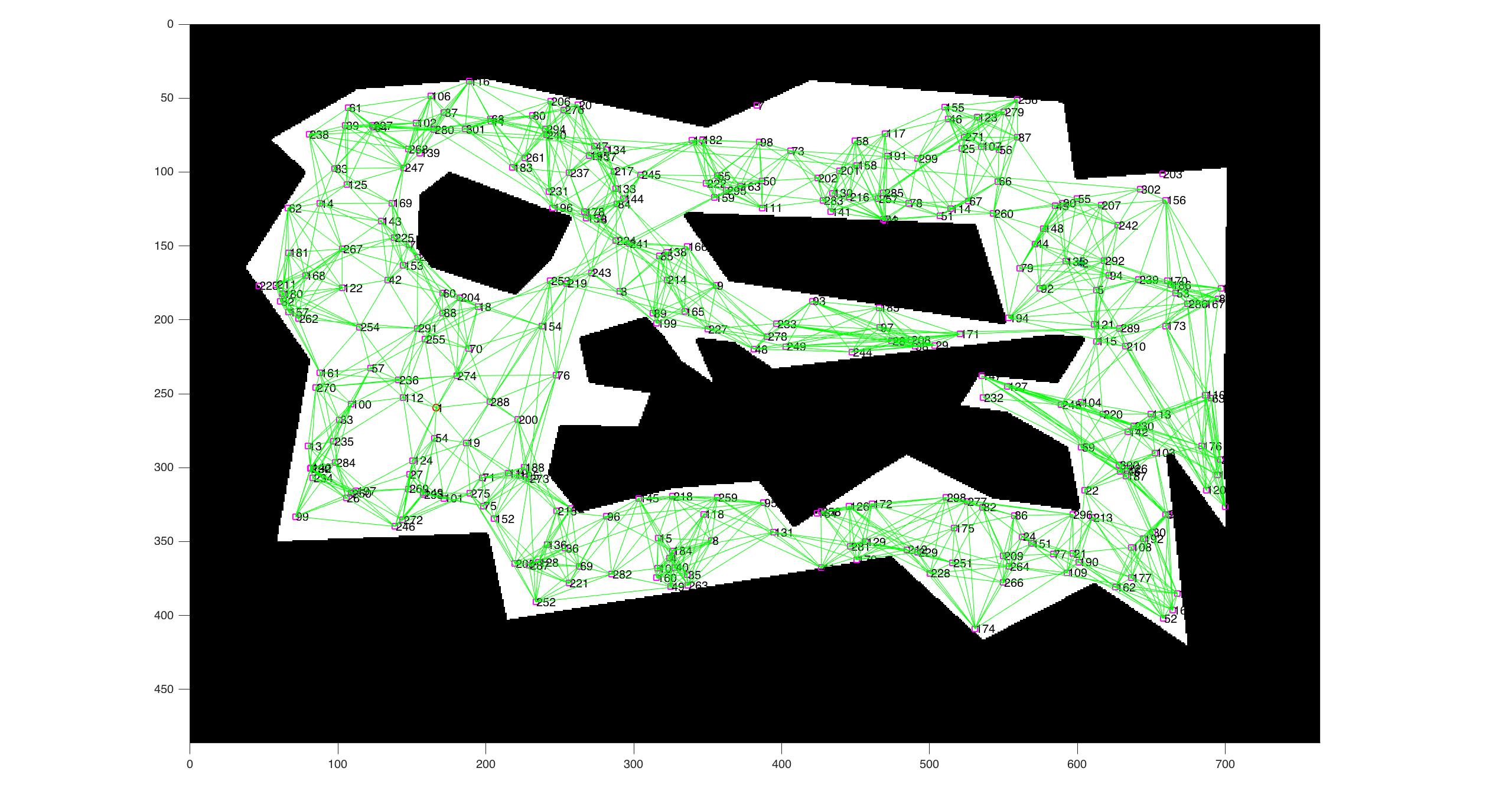
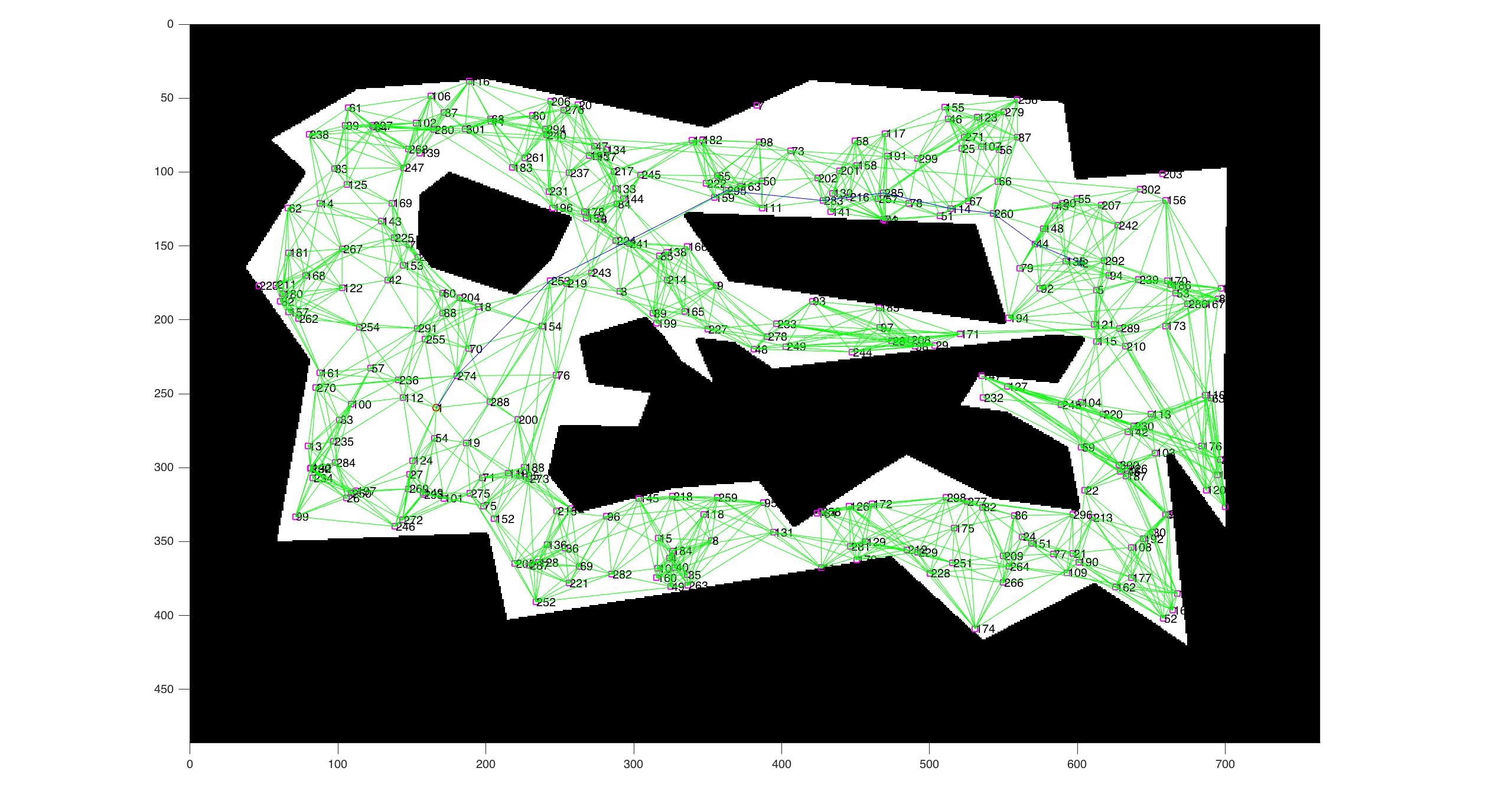
The graph generated depends on two variables. The number of samples we want to generate and the graph connectivity.
For a small connectivity we will have the following result:

And the opposite would be:
After generating the graph we check if there exists a route between the starting node and the goal node. If it exists we compute the shortest path with Dijkstra’s algorithm. This will give us the Path of nodes a1,a2…an.
Reactive Navigation
With these nodes we proceed to execute the reactive navigation.
The local (or reactive) navigation is done using Potential Fields. Each obstacle in a distance of less than a certain threshold will affect the robot’s path. Also, the goal objective will push our robot towards it with a certain force.
The formula too compute the force is not unique, we can come up with any sort of way to make an obstacle affect the robot’s movement. For example, for the repulsion we could use the following:
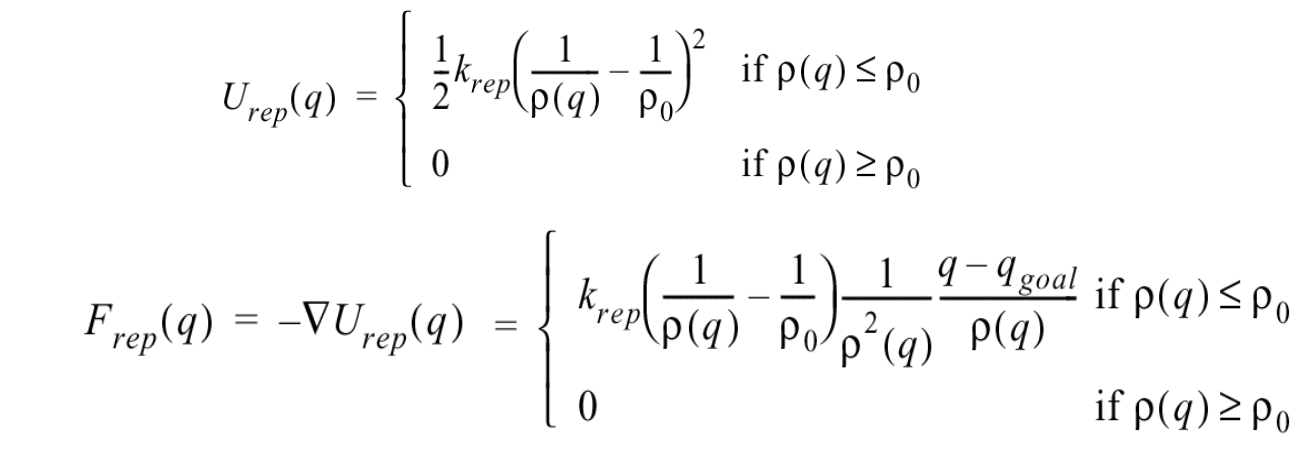
And for the attracting force we could use something similar. Then the total force would be the sum of both forces (keep in mind that since we are working on a 2D plane, the force is a vector).
This is an example of navigation:
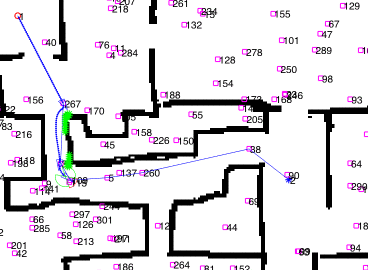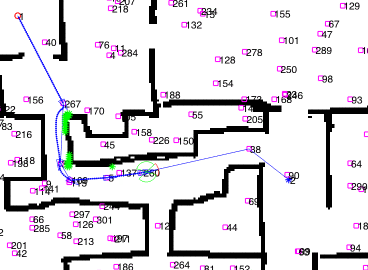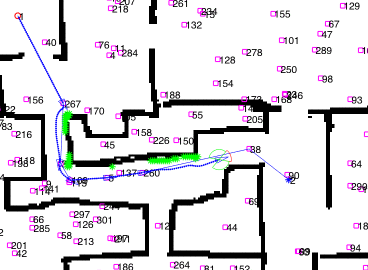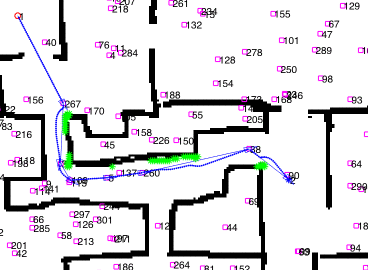
Optimizations
The straightforward implementation would be VERY SLOW.
For the global navigation, lets suppose we want to compute if there is an edge between two nodes. We would have to check if there is a straight line that does not intersect with any obstacle right?
The brute force approach to this problem would be to check for every cell of the grid that is inbetween both points if the line intersects with an obstacle. This is SLOW.
A faster approach would be to compute Bresenham’s algorithm to check the pixels that the straight line crosses and then only check those cells if they are obstacles or not.
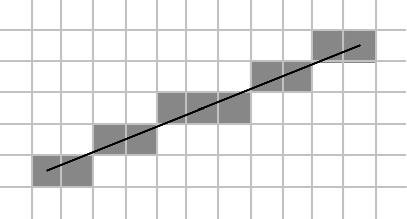
Local Navigation Optimization
The Potential Fields tecnhique takes into account ALL the obstacles in the map.
Therefore instead of considering all we could consider only a small window between each navigation. So that the program is scalable for bigger maps.
Also to make it more realistic, the use of a fov (Field-Of-View) would be nice so that the robot is limited with the effective distance and bearing of the given sensor.